EQUAL STACK

You have three stacks of cylinders where each cylinder has the same diameter, but they may vary in height. You can change the height of a stack by removing and discarding its topmost cylinder any number of times.

Find the maximum possible height of the stacks such that all of the stacks are exactly the same height. This means you must remove zero or more cylinders from the top of zero or more of the three stacks until they're all the same height, then print the height. The removals must be performed in such a way as to maximize the height.

Note: An empty stack is still a stack.

Input Format

The first line contains three space-separated integers, , , and , describing the respective number of cylinders in stacks , , and . The subsequent lines describe the respective heights of each cylinder in a stack from top to bottom:

• The second line contains  space-separated integers describing the cylinder heights in stack .
• The third line contains  space-separated integers describing the cylinder heights in stack .
• The fourth line contains  space-separated integers describing the cylinder heights in stack .

Constraints

Output Format

Print a single integer denoting the maximum height at which all stacks will be of equal height.

Sample Input

5 3 4
3 2 1 1 1
4 3 2
1 1 4 1

Sample Output

5

Explanation

Initially, the stacks look like this:

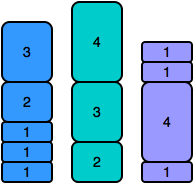
Observe that the three stacks are not all the same height. To make all stacks of equal height, we remove the first cylinder from stacks  and , and then remove the top two cylinders from stack  (shown below).

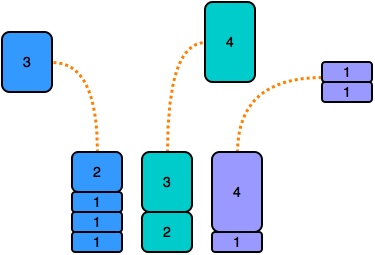
As a result, the stacks undergo the following change in height:

All three stacks now have . Thus, we print  as our answer.

CLICK HERE FOR SOLUTION