Kruskal’s Minimum Spanning Tree Algorithm & Programme

PROBLEM : 

                Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest. It is a greedy algorithm in graph theory as it finds a minimum spanning tree for a connected weighted graph adding increasing cost arcs at each step.

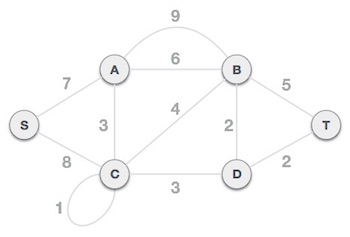
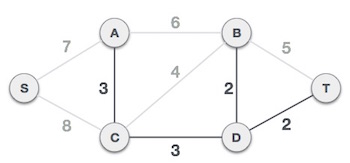
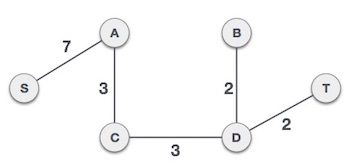
To understand Kruskal's algorithm let us consider the following example −

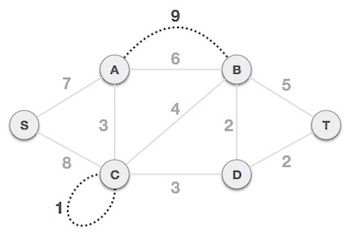
Step 1 - Remove all loops and Parallel Edges

Remove all loops and parallel edges from the given graph.

In case of parallel edges, keep the one which has the least cost associated and ove all others.

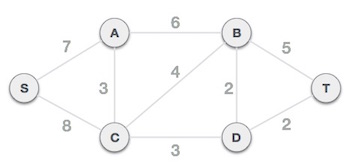
Step 2 - Arrange all edges in their increasing order of weight

The next step is to create a set of edges and weight, and arrange them in an ascending order of weightage (cost).

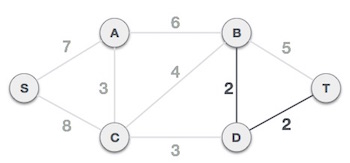
Step 3 - Add the edge which has the least weightage

Now we start adding edges to the graph beginning from the one which has the least weight. Throughout, we shall keep checking that the spanning properties remain intact. In case, by adding one edge, the spanning tree property does not hold then we shall consider not to include the edge in the graph.

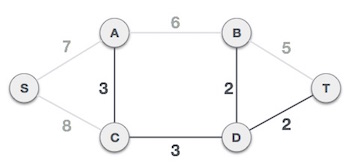
The least cost is 2 and edges involved are B,D and D,T. We add them. Adding them does not violate spanning tree properties, so we continue to our next edge selection.

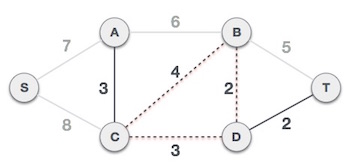
Next cost is 3, and associated edges are A,C and C,D. We add them again −

Next cost in the table is 4, and we observe that adding it will create a circuit in the graph. −

We ignore it. In the process we shall ignore/avoid all edges that create a circuit.

We observe that edges with cost 5 and 6 also create circuits. We ignore them and move on.

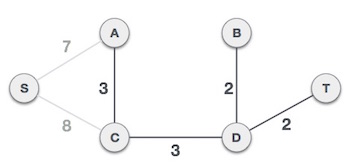
Now we are left with only one node to be added. Between the two least cost edges available 7 and 8, we shall add the edge with cost 7.

By adding edge S,A we have included all the nodes of the graph and we now have minimum cost spanning tree.

CLICK HERE TO DOWNLOAD THE PROGRAM

PROGRAM:

#include<stdio.h>
#include<stdlib.h>
int count=0;
struct edge
{
    int startVer;
    int endVer;
    int weight;
};
struct graph
{
    struct edge * ed;
    struct graph *next;
}*head=NULL;
struct set
{
    int ver;
    int setNo;
    struct set * nextVer;
}*headSet=NULL;
void addVertex(int i)
{
    struct set *s=(struct set *)malloc(sizeof(struct set *));
    s->ver=i;
    s->setNo=i;
    s->nextVer=NULL;
    s->nextVer=headSet;
    headSet=s;
}
printVertex()
{
    struct set * t;
    t=headSet;
    while (t!=NULL)
    {
        printf("%d \n",t->ver);
          printf("%d \n",t->setNo);
        t=t->nextVer;
    }
}
void addEdge()
{
    int start,end,w;

    struct graph *g=(struct graph *)malloc(sizeof(struct graph *));
    struct edge *e=(struct edge *)malloc(sizeof(struct edge *));


    printf("START VERTEX:");
    scanf("%d",&start);
    e->startVer=start;

    printf("END VERTEX:");
    scanf("%d",&end);
    e->endVer=end;

    printf("ENTER WEIGHT :");
    scanf("%d",&w);
    e->weight=w;

    g->ed=e;

    g->next=NULL;
    g->next=head;
    head=g;
    count++;
}
void view()
{
    struct graph *t;
    t=head;
    if (head==NULL)
    {
        printf("\n******EMPTY LINK LIST*******\n");
        return;
    }
    while (t!=NULL)
    {
        printf ("%d %d %d\n",t->ed->startVer,t->ed->endVer,t->ed->weight);
        t=t->next;
    }
}
void sort()
{
    if(head==NULL)
   {
   printf("\n********EMPTY LINK LIST*******\n");
  return ;
  }
int i,j;
struct edge *q;
struct graph *p;
p=head;
for (i=0;i<count;i++)
{
    for (j=0;j<count-1;j++)
    {
        if(p->ed->weight > p->next->ed->weight)
        {
        q=p->ed;
        p->ed=p->next->ed;
        p->next->ed=q;


        }
         p=p->next;
    }
    p=head;
}
}
void unionSet(int u,int v)
{
    int x=findset(u);
    struct set *ref;
    ref=headSet;
    while(ref->ver!=v)
    {
        ref=ref->nextVer;
    }
    int y=ref->setNo;
    ref->setNo=x;

    ref=headSet;
    while(ref!=NULL)
    {
        if(ref->setNo==y)
        {
            ref->setNo=x;
        }
        ref=ref->nextVer;

    }

    printf("FOR X: %d Y: %d ",u,v);
    printf("SET NO OF U :- %d",x);
    printf(" SET NO OF U :- %d\n",y);
}
int findset(int v)
{
    struct set *ref;
    ref=headSet;
    while(ref->ver!=v)
    {
        ref=ref->nextVer;
    }


    return (ref->setNo);
}
krushkal()
{
    struct graph *g=NULL;
    struct edge *e=NULL;
    sort();
    view();
    g=head;
    while(g!=NULL)
    {
        e=g->ed;
        if(findset(e->startVer)!=findset(e->endVer))
        {
            printf("EDGE [%d][%d] \n",e->startVer,e->endVer);
            unionSet(e->startVer,e->endVer);
        }
        g=g->next;
    }
}
main()
{
    int n,i,j,choise;
    int isdirected,weight;
    printf("ENTER THE TOTAL VERTICES : ");
    scanf("%d",&n);
    for(i=0;i<n;i++)
    {
        addVertex(i);
    }
    printVertex();
    while(1)
    {
        printf("\nMENU:\n1-ADD THE EDGE IN THE GRAPH\n2- FIND KRUSHKAL\n3-EXIT\n");
        scanf("%d",&choise);
        switch(choise)
        {
            case 1:addEdge();break;
            case 2:krushkal();break;
            case 3:exit(0);
        }
        view();
    }
}

Reference